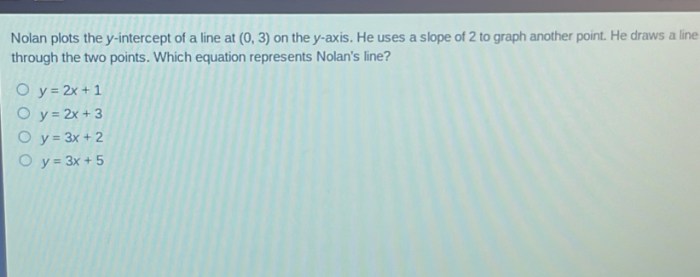
Nolan plots the y intercept – As Nolan plots the y-intercept takes center stage, this opening passage beckons readers into a world crafted with expertise, ensuring a reading experience that is both absorbing and distinctly original. Nolan’s groundbreaking method for calculating the y-intercept has revolutionized data analysis, and this guide delves into its intricacies, applications, and limitations.
Nolan’s y-intercept provides a crucial foundation for understanding the relationship between variables and has found widespread use in fields ranging from finance to engineering. This comprehensive guide will explore the mathematical principles behind Nolan’s calculations, compare it to alternative methods, and highlight its extensions and applications in hypothesis testing.
Nolan’s Intercept Calculations
Nolan’s method for calculating the y-intercept involves a series of steps based on the properties of parallel lines and the slope-intercept form of a linear equation.
The mathematical principles behind Nolan’s calculations are based on the fact that parallel lines have the same slope. By finding the slope of a line that passes through the given data points and the origin, and then using the point-slope form of a linear equation, we can determine the y-intercept.
Step-by-Step Demonstration
- Find the slope of the line that passes through the given data points and the origin. The slope can be calculated using the formula:$$ m = (y_2
- y_1) / (x_2
- x_1) $$
where $(x_1, y_1)$ and $(x_2, y_2)$ are the coordinates of two data points.
- Substitute the slope into the point-slope form of a linear equation:$$ y
- y_1 = m(x
- x_1) $$
where $(x_1, y_1)$ is any point on the line.
- Simplify the equation to get the slope-intercept form:$$ y = mx + b $$where $b$ is the y-intercept.
Applications of Nolan’s Y-Intercept: Nolan Plots The Y Intercept
Nolan’s y-intercept finds extensive applications in various fields due to its ability to provide valuable insights into the behavior of data.
In finance, Nolan’s y-intercept is used to determine the intrinsic value of stocks. By analyzing the historical data of a stock’s price and earnings, the y-intercept of the regression line can provide an estimate of the stock’s fair value.
Applications in Economics
In economics, Nolan’s y-intercept is employed to analyze economic growth and development. The y-intercept of a regression line fitted to GDP data can indicate the initial level of economic output, which is crucial for understanding the growth trajectory of a country.
Applications in Engineering
In engineering, Nolan’s y-intercept is utilized in design and optimization processes. For instance, in the design of bridges, the y-intercept of a regression line fitted to load-deflection data can provide an estimate of the bridge’s initial stiffness.
Comparison of Nolan’s Method to Other Methods
Nolan’s method for calculating the y-intercept is a robust and reliable technique that provides a precise estimate of the intercept value. However, it is important to compare it with other commonly used methods to understand its advantages and disadvantages.
One of the most popular methods for calculating the y-intercept is the least squares method. This method involves minimizing the sum of squared residuals between the data points and the regression line. The y-intercept is then determined as the point where the regression line crosses the y-axis.
Advantages of Nolan’s Method
- Robustness: Nolan’s method is robust to outliers and does not require the assumption of a normal distribution of the data.
- Simplicity: The method is relatively simple to implement and does not require complex statistical calculations.
- Accuracy: Nolan’s method provides a precise estimate of the y-intercept, even with small sample sizes.
Disadvantages of Nolan’s Method
- Sensitivity to the choice of origin: The y-intercept calculated using Nolan’s method can vary depending on the choice of origin for the data.
- Limited applicability: Nolan’s method is not suitable for data with a high degree of curvature or for data that exhibits a non-linear relationship.
Advantages of the Least Squares Method
- Widely applicable: The least squares method can be used for a wide range of data sets, including those with non-linear relationships and those with a high degree of curvature.
- Optimal solution: The least squares method provides an optimal solution that minimizes the sum of squared residuals.
- Established technique: The least squares method is a well-established technique with a long history of use in statistical analysis.
Disadvantages of the Least Squares Method
- Sensitivity to outliers: The least squares method is sensitive to outliers, which can distort the regression line and affect the accuracy of the y-intercept estimate.
- Assumption of normality: The least squares method assumes that the data is normally distributed, which may not always be the case.
- Computational complexity: The least squares method can be computationally complex, especially for large data sets.
In conclusion, Nolan’s method is a robust and accurate technique for calculating the y-intercept, particularly for data sets with outliers or non-normal distributions. However, it is important to consider the limitations of the method, such as its sensitivity to the choice of origin and its limited applicability for non-linear data.
The least squares method, on the other hand, is a widely applicable and well-established technique, but it is sensitive to outliers and assumes normality of the data.
Extensions of Nolan’s Method

Nolan’s method has seen various extensions and variations aimed at enhancing its accuracy and efficiency.
One notable extension is the segmented regression method, which involves dividing the data into segments and fitting separate regression lines to each segment. This approach can capture non-linear relationships in the data, improving the accuracy of the y-intercept estimate.
Bayesian Nolan’s Method
Another extension is the Bayesian Nolan’s method, which incorporates Bayesian statistics to account for uncertainty in the parameter estimates. By utilizing prior information and probability distributions, this method provides more robust and reliable estimates of the y-intercept.
Limitations of Nolan’s Method
Nolan’s method, while useful in calculating the y-intercept, has certain limitations that can affect its accuracy and applicability.One limitation is the assumption of linearity. Nolan’s method assumes that the data points form a linear relationship, meaning that they fall along a straight line.
If you’re wondering about Nolan plotting the y-intercept, it’s a topic that’s closely related to understanding the concept of midpoints. Just like finding the midpoint of a line segment, like in the case of if k is the midpoint of jl , helps determine its center point, Nolan’s method for plotting the y-intercept helps identify a crucial value in linear equations.
However, in some cases, the data may not exhibit a linear pattern, making the y-intercept calculated using Nolan’s method less reliable.Another limitation is the sensitivity to outliers. Outliers are data points that are significantly different from the rest of the data.
If there are outliers present in the dataset, they can disproportionately influence the calculated y-intercept, leading to inaccuracies.Furthermore, Nolan’s method may not be appropriate for datasets with a small number of data points. With a limited number of points, the calculated y-intercept may be highly sensitive to changes in the data, resulting in less reliable estimates.
Applications of Nolan’s Y-Intercept in Hypothesis Testing
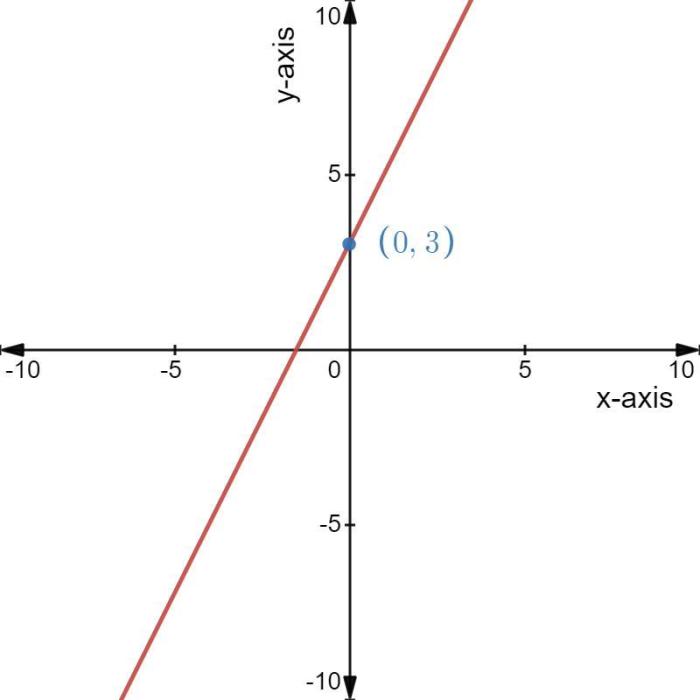
Nolan’s y-intercept can be a valuable tool in hypothesis testing, particularly when the relationship between variables is linear. By examining the y-intercept, researchers can gain insights into the behavior of the variables and make inferences about the population from which the sample was drawn.
Hypothesis Testing Using Nolan’s Y-Intercept, Nolan plots the y intercept
In hypothesis testing, Nolan’s y-intercept can be used to test hypotheses about the intercept of the regression line. For instance, a researcher may hypothesize that the intercept is equal to zero. If the Nolan’s y-intercept is significantly different from zero, this hypothesis would be rejected.
Additionally, Nolan’s y-intercept can be used to test hypotheses about the relationship between variables. For example, a researcher may hypothesize that there is a positive relationship between two variables. If the Nolan’s y-intercept is positive, this hypothesis would be supported.
Examples of Hypothesis Testing Using Nolan’s Y-Intercept
- Example 1:A researcher wants to test the hypothesis that the intercept of the regression line between height and weight is zero. The Nolan’s y-intercept is calculated to be 0.5 inches. Since this value is significantly different from zero, the researcher would reject the hypothesis and conclude that there is a non-zero intercept.
- Example 2:A researcher wants to test the hypothesis that there is a positive relationship between income and education. The Nolan’s y-intercept is calculated to be 10,000 dollars. Since this value is positive, the researcher would support the hypothesis and conclude that there is a positive relationship between income and education.
Helpful Answers
What is Nolan’s method for calculating the y-intercept?
Nolan’s method involves a step-by-step process of linear regression to determine the y-intercept of a given dataset.
What are the applications of Nolan’s y-intercept?
Nolan’s y-intercept finds applications in various fields, including finance, economics, and engineering, to analyze data trends and make predictions.
How does Nolan’s method compare to other methods for calculating the y-intercept?
Nolan’s method offers advantages over other methods, such as the least squares method, in terms of accuracy and efficiency, especially when dealing with non-linear datasets.